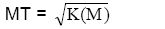Jika diketahui lingkaran L adalah (x – a)2 + (y – b)2 = r2 dan terdapat titik M(x1, y1) diluar lingkaran L, maka kuasa titik M terhadap lingkaran L dirumuskan :
K(M) = (x1 – a)2 + (y1– b)2 – r2
Nilai kuasa ini menunjukkan kuadrat jarak dari titik M ke titik T.
Sedangkan untuk lingkaran x2 + y2 + Ax + By + C = 0, kuasa titik M( x1 , y1 ) dirumuskan K(M) = x12 + y12 + A x1 + B y1 + C

Jika M titik diluar lingkaran dan g adalah garis singgung lingkaran yang ditarik dari M serta T adalah adalah titik singgungnya, maka dirumuskan:

K(M) = (x1 – a)2 + (y1– b)2 – r2
Nilai kuasa ini menunjukkan kuadrat jarak dari titik M ke titik T.
Sedangkan untuk lingkaran x2 + y2 + Ax + By + C = 0, kuasa titik M( x1 , y1 ) dirumuskan K(M) = x12 + y12 + A x1 + B y1 + C

Jika M titik diluar lingkaran dan g adalah garis singgung lingkaran yang ditarik dari M serta T adalah adalah titik singgungnya, maka dirumuskan:
Untuk pemahaman lebih lanjut ikutilah contoh soal berikut ini :
01. Tentukanlah nilai kuasa titik A(–3, 2) terhadap lingkaran x2 + y2 – 10x + 6y + 18 = 0
Jawab
K(A) = x12 + y12 + A x1 + B y1 + C
K(A) = (–3)2 + (2)2 – 10(–3) + 6(2) + 18
K(A) = 9 + 4 + 30 + 12 + 18
K(A) = 73
02. Diketahui lingkaran berpusat di P(2, 4) dan berjari jari r. Jika kuasa lingkaran tersebut di titik A(6, –1) bernilai 16, maka tentukanlah persamaan lingkarannya
Jawab
K(A) = 16
( x1 – 2)2 + ( y1 – 4)2 – r2 = 16
(6 – 2)2 + (–1 – 4)2 – r2 = 16
16 + 25 – r2 = 16
r2 = 25
Persamaannya:
(x – 2)2 + (y – 4)2 = 25
x2 – 4x + 4 + y2 – 8y + 16 = 25
x2 + y2 – 4x – 8y – 5 = 0
03. Diketahui lingkaran x2 + y2 – 10x + 6y + 18 = 0. Jika kuasa titik A (10, p) terhadap lingkaran tersebut adalah 34, maka nilai p = ….
Jawab
K(A) = 34 x12 + y12 – 10 x1 + 6 y1 + 18 = 34
(10)2 + (p)2 – 10(10) + 6(p) + 18 = 34
100 + p2 – 100 + 6p + 18 – 34 = 0
p2 + 6p – 16 = 0
(p + 8)(p – 6) = 0
Nilai p = –8 dan p = 6
Tiga kemungkinan kedudukan titik terhadap lingkaran L
1. Titik A(x, y) terletak di dalam lingkaran jika K(A) < ruas kanan
2. Titik B(x, y) terletak pada lingkaran jika K(B) = ruas kanan
3. Titik C(x, y) terletak di luar lingkaran jika K(C) > ruas kanan
Sebagai contoh diketahui lingkaran (x – 2)2 + (y + 4)2 = 40, maka
Titik P(5, 1) terletak di dalam lingkaran karena (5 – 2)2 + (1 + 4)2 =34 < 40
Titik P(8, -2) terletak tepat pada lingkaran karena (8 – 2)2 + (-2 + 4)2 = 40 = 40
Titik P(-3, 2) terletak di luar lingkaran karena (-3 – 2)2 + (2 + 4)2 = 61> 40
Untuk lingkaran x2 + y2 + 6x – 4y – 23 = 0, maka
Titik P(2, 5) terletak di dalam lingkaran karena 22 + 52 + 6.2 – 4.5 – 23 = – 2 < 0
Titik P(3, 2) terletak tepat pada lingkaran karena 32 + 22 + 6.3 – 4.2 – 23 = 0 = 0
Titik P(4, -1) terletak di luar lingkaran karena 42 + (-1)2 + 6.4 – 4(-1) – 23 = 16 > 0
Untuk lebih jelasnya, pelajarilah contoh soal berikut ini:
04. Jika diketahui titik T(k, 3) terletak pada lingkaran x2 + y2– 13x + 5y + 6 = 0 maka tentukanlah nilai k
Jawab
x2 + y2 – 13x + 5y + 6 = 0
(k)2 + (3)2 – 13(k) + 5(3) + 6 = 0
k2 + 9 – 13k + 15 + 6 = 0
k2 – 13k + 12 = 0
(k – 12)(k – 1) = 0
Jadi nilai k = 12 dan k = 1
Jika M( x1 , y1 ) titik diluar lingkaran serta a dan b adalah garis singgung lingkaran yang ditarik dari M maka:
M dinamakan titik polar
g dinamakan garis polar
Contoh soal
08. Tentukan persamaan garis polar terhadap lingkaran x2 + y2 – 8x + 6y + 9 = 0. yang ditarik dari titik A (–2, 5)
Jawab

Kedudukan garis g terhadap lingkaran L ditentukan oleh nilai diskriminan D = b2 – 4ac, hasil dari substitusi persamaan lingkaran dan persamaan garis. Ketentuannya :
1. D > 0 garis g memotong lingkaran L di dua titik persekutuan
2. D = 0 garis g menyinggung lingkaran L di satu titik
3. D < 0 garis g di luar lingkaran L
Sebagai contoh kedudukan garis y = 3x – 2 terhadap lingkaran x2 + y2 – 8x – 2y + 15 = 0 adalah berpotongan didua titik, karena memenuhi aturan:
x2 + (3x – 2)2 – 8x – 2(3x – 2) + 15
= x2 + 9x2 – 12x + 4 – 8x – 6x + 4 + 15
= 10x2 + 4x – 16
= 5x2 + 2x – 8
Tinjau D = 22 – 4(5)(-8) = 164 > 0
Karena D > 0 maka garis y = 3x – 2 memotong lingkaran x2 + y2 – 8x – 2y + 15 = 0 di dua titik
Untuk lebih jelasnya, pelajarilah contoh soal berikut ini:
10. Tentukanlah kedudukan garis y = x – 2 terhadap lingkaran (x – 3)2 + (y + 4)2 = 9
Jawab
11. Jika garis y = x + 9 menyinggung lingkaran x2 + y2 + 8x – 10y + 21 – p = 0 di satu titik maka tentukanlah nilai p
Jawab
12. Buktikan bahwa garis y = 2x + 1 memotong lingkaran x2 + y2 + 4x + 6y + 8 = 0 dan tentukanlah titik potongnya
Jawab
Thanks for reading & sharing .