Bentuk umum sistem persamaan linier dan kuadrat :
y = ax + b
y = ax2 + bx + c
Dalam grafik cartesius, titik potong antara garis dan parabola merupakan penyelesaian sistem persamaan itu.
Metoda menyelesaikan sistem persamaan ini adalah metoda substitusi dan eliminasi
Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
01. Tentukan penyelesaian dari sistem persamaan y = x2 + 5x – 4 dan y = 3x + 4
Jawab
y = y
x2 + 5x – 4 = 3x + 4
x2 + 5x – 4 – 3x – 4 = 0
x2 + 2x – 8 = 0
(x + 4)(x – 2) = 5
x1 = –4 dan x2 = 2
Untuk x1 = –4 maka y1 = 3x1 + 4 = 3(–4) + 4 = –8
Untuk x2 = 2 maka y2 = 3x2 + 4 = 3(2) + 4 = 10
Jadi H = {(–4, –8), (2, 10)}
02. Tentukan penyelesaian dari sistem persamaan y = x2 + 2x + 5 dan 3x + 2y = 7
Jawab
y = x2 + 2x + 5 dan 3x + 2y = 7
Sehingga:
3x + 2y = 7
3x + 2(x2 + 2x + 5) = 7
3x + 2x2 + 4x + 10 = 7
2x2 + 7x + 3 = 0
(2x + 1)(x + 3) = 5
x1 = –1/2 dan x2 = –3
Untuk x1 = –1/2 maka 3x1 + 2y1 = 7
3(–1/2) + 2y1 = 7
–3/2 + 2y1 = 7
2y1 = 17/2 maka y1 = 17/4
Untuk x2 = –3 maka 3x2 + 2y2 = 7
3(–3) + 2y2 = 7
–9 + 2y2 = 7
2y2 = 16
y2 = 8
Jadi H = {(–1/2, 17/4), (–3, 8)}
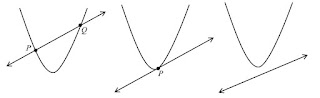
Jika ditinjau dari gambar grafiknya, maka terdapat tiga macam kemungkinan penyelesaian sistim persamaan linier dan kuadrat.
Ketiga macam penyelesaian ini diperoleh dari analisa diskriminan (D) hasil substitusi persamaan linier dan kuadrat, yakni:
untuk D > 0 mempunyai dua titik penyelesaian
untuk D = 0 mempunyai satu titik penyelesaian
untuk D < 0 tidak mempunyai titik penyelesaian
Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
03. Jika sistem persamaan y = x2 – 4x + 3p dan y = 2x + 3 mempunyai satu titik penyelesaian, maka tentukanlah nilai p
Jawab
y = y
x2 – 4x + 3p = 2x + 3
x2 – 4x + 3p – 2x – 3 = 0
x2 – 6x + 3p – 3 = 0
Syarat :
D = b2 – 4ac = 0
(–6)2 – 4(1)(3p – 3) = 0
36 – 4(3p – 3) = 0
36 – 12p + 12 = 0
–12p + 48 = 0
–12p = –48
p = 4
Sistem persamaan linier dan kuadrat banyak dipakai dalam kehidupan sehari-hari, antara lain dalam bidang fisika. Beberapa diantaranya akan diuraikan pada contoh soal berikut ini:
01. Keliling sebuah persegi panjang adalah 18 cm. Jika panjang dan lebarnya bertambah 2 cm, maka luas persegipanjang tersebut menjadi 42 cm2. Carilah ukuran persegi panjang tersebut
Jawab
Misalkan panjang persegi panjang = p dan lebarnya = l, maka
Keliling = 2 (p + l) = 18
p + l = 9
l = 9 – p ............................................................................ (1)
Setelah panjang dan lebar ditambah 2, maka luas persegi panjang menjadi
Luas = (p + 2) (l + 2) = 42 ............................................... (2)
Substitusikan persamaan (1) ke (2) diperoleh
(p + 2) (9 – p + 2) = 42
(p + 2) (11 – p) = 42
11p – p2 + 22 – 2p = 42
11p – p2 + 22 – 42 = 0
p2 – 9p – 20 = 0
(p – 4)(p – 5) = 0
Jadi p = 5 cm dan l = 9 – 5 = 4 cm
02. Diketahui jumlah dua bilangan adalah 9. Jika jumlah kuadrat kedua bilangan itu adalah 41, maka tentukanlah selisih kedua bilangan tersebut
Jawab
Misalkan kedua bilangan itu adalah x dan y, maka
x + y = 9 y = 9 – x ….……………………… (1)
x2 + y2 = 41 …………………………………(2)
Jika disubstitusikan (1) ke (2) diperoleh :
x2 + (9 – x)2 = 41
x2 + 81 – 2x + x2 = 41
2x2 – 2x + 40 = 0
x2 – x + 20 = 0
(x – 4)(x – 5) = 0
Untuk x = 4 diperoleh y = 9 – 4 = 5
Untuk x = 5 diperoleh y = 9 – 5 = 4
Jadi kedua bilangan itu adalah 4 dan 5, sehingga selisihnya : 5 – 4 = 1
y = ax + b
y = ax2 + bx + c
Dalam grafik cartesius, titik potong antara garis dan parabola merupakan penyelesaian sistem persamaan itu.
Metoda menyelesaikan sistem persamaan ini adalah metoda substitusi dan eliminasi
Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
01. Tentukan penyelesaian dari sistem persamaan y = x2 + 5x – 4 dan y = 3x + 4
Jawab
y = y
x2 + 5x – 4 = 3x + 4
x2 + 5x – 4 – 3x – 4 = 0
x2 + 2x – 8 = 0
(x + 4)(x – 2) = 5
x1 = –4 dan x2 = 2
Untuk x1 = –4 maka y1 = 3x1 + 4 = 3(–4) + 4 = –8
Untuk x2 = 2 maka y2 = 3x2 + 4 = 3(2) + 4 = 10
Jadi H = {(–4, –8), (2, 10)}
02. Tentukan penyelesaian dari sistem persamaan y = x2 + 2x + 5 dan 3x + 2y = 7
Jawab
y = x2 + 2x + 5 dan 3x + 2y = 7
Sehingga:
3x + 2y = 7
3x + 2(x2 + 2x + 5) = 7
3x + 2x2 + 4x + 10 = 7
2x2 + 7x + 3 = 0
(2x + 1)(x + 3) = 5
x1 = –1/2 dan x2 = –3
Untuk x1 = –1/2 maka 3x1 + 2y1 = 7
3(–1/2) + 2y1 = 7
–3/2 + 2y1 = 7
2y1 = 17/2 maka y1 = 17/4
Untuk x2 = –3 maka 3x2 + 2y2 = 7
3(–3) + 2y2 = 7
–9 + 2y2 = 7
2y2 = 16
y2 = 8
Jadi H = {(–1/2, 17/4), (–3, 8)}
Jika ditinjau dari gambar grafiknya, maka terdapat tiga macam kemungkinan penyelesaian sistim persamaan linier dan kuadrat.
Ketiga macam penyelesaian ini diperoleh dari analisa diskriminan (D) hasil substitusi persamaan linier dan kuadrat, yakni:
untuk D > 0 mempunyai dua titik penyelesaian
untuk D = 0 mempunyai satu titik penyelesaian
untuk D < 0 tidak mempunyai titik penyelesaian
Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
03. Jika sistem persamaan y = x2 – 4x + 3p dan y = 2x + 3 mempunyai satu titik penyelesaian, maka tentukanlah nilai p
Jawab
y = y
x2 – 4x + 3p = 2x + 3
x2 – 4x + 3p – 2x – 3 = 0
x2 – 6x + 3p – 3 = 0
Syarat :
D = b2 – 4ac = 0
(–6)2 – 4(1)(3p – 3) = 0
36 – 4(3p – 3) = 0
36 – 12p + 12 = 0
–12p + 48 = 0
–12p = –48
p = 4
Sistem persamaan linier dan kuadrat banyak dipakai dalam kehidupan sehari-hari, antara lain dalam bidang fisika. Beberapa diantaranya akan diuraikan pada contoh soal berikut ini:
01. Keliling sebuah persegi panjang adalah 18 cm. Jika panjang dan lebarnya bertambah 2 cm, maka luas persegipanjang tersebut menjadi 42 cm2. Carilah ukuran persegi panjang tersebut
Jawab
Misalkan panjang persegi panjang = p dan lebarnya = l, maka
Keliling = 2 (p + l) = 18
p + l = 9
l = 9 – p ............................................................................ (1)
Setelah panjang dan lebar ditambah 2, maka luas persegi panjang menjadi
Luas = (p + 2) (l + 2) = 42 ............................................... (2)
Substitusikan persamaan (1) ke (2) diperoleh
(p + 2) (9 – p + 2) = 42
(p + 2) (11 – p) = 42
11p – p2 + 22 – 2p = 42
11p – p2 + 22 – 42 = 0
p2 – 9p – 20 = 0
(p – 4)(p – 5) = 0
Jadi p = 5 cm dan l = 9 – 5 = 4 cm
02. Diketahui jumlah dua bilangan adalah 9. Jika jumlah kuadrat kedua bilangan itu adalah 41, maka tentukanlah selisih kedua bilangan tersebut
Jawab
Misalkan kedua bilangan itu adalah x dan y, maka
x + y = 9 y = 9 – x ….……………………… (1)
x2 + y2 = 41 …………………………………(2)
Jika disubstitusikan (1) ke (2) diperoleh :
x2 + (9 – x)2 = 41
x2 + 81 – 2x + x2 = 41
2x2 – 2x + 40 = 0
x2 – x + 20 = 0
(x – 4)(x – 5) = 0
Untuk x = 4 diperoleh y = 9 – 4 = 5
Untuk x = 5 diperoleh y = 9 – 5 = 4
Jadi kedua bilangan itu adalah 4 dan 5, sehingga selisihnya : 5 – 4 = 1
Thanks for reading & sharing .