
Pada gambar di atas, misalkan luas daerah yang dibatasi oleh kurva y = f(x) dan sumbu-X, dalam interval x= a dan x = b dinamakan D, maka D dapat dicari pendekatannya dengan menghitung luas persegi pangjang-persegi panjang yang melingkupinya (seperti gambar di atas).
Dari gambar di atas, lebar persegi panjang- persegi panjang dibuat sama yakni xi sedangkan panjangnya f(xi)
(dimana i = 1, 2, 3 dan 4), sehinga luas persegi panjang keseluruhan dirumuskan:

Pendekatan mentukan luas dengan menggunakan deret diatas dinamakan pendekatan Rienman. Tentu saja luas L yang didapat tidak akan sama dengan luas D yang sebenarnya. Semakin banyak persegi panjang yang digunakan, akan membuat nilai L semakin mendekati luas D yang sebenarnya.
Sebagai contoh akan dihitung luas daerah yang dibatasi oleh kurva y = x2 + 2 dan sumbu-X dalam interval x = 1 dan x = 5 menggunakan pendekatan deret Rieman dengan empat persegi panjang

Jawab
L = f(1)Δx + f(2)Δx + f(3)Δx + f(4)Δx
L = (3)(1) + (6)(1) + (11)(1) + (18)(1)
L = 38 satuan luas
Jika banyaknya persegipanjang ditambah menjadi 8, 16, 32 dan seterusnya, maka nilai L yang didapat akan mendekati luas yang sebenarnya.

Pada tabel di atas tampak bahwa jika persegi panjang dibuat sebanyak 256 buah maka luasnya menjadi 49,145 satuan luas.
Jika persegi panjang itu dibuat sebanyak tak hingga buah, maka lebar persegi panjang, yakni Δx menjadi sangat kecil (mendekati nol) dan persegi panjang-persegi panjang itu hampir berbentuk garis yang jumlahnya tak hingga. Sehingga luas L dapat dianggap sama dengan luas D.
Untuk lebih jelasnya akan diuraikan dalam contoh soal berikut ini:
01. Tentukanlah luas daerah yang diarsir pada gambar dibawah dengan pendekatan integral dan dengan rumus luas
Jawab


02. Tentukan luas daerah yang diarsir pada gambar berikut jika dihitung dengan pendekatan:
(a) Integral tentu
(b) Deret Rienman menggunakan 6 persegi panjang

Jawab


03. Hitunglah

Jawab
= [4(3)3 – 4(3)2 +3] – [4(2)3 – 4(2)2 +2]
= [108 – 36 + 3] – [32 – 16 + 2]
= 75 – 18
= 57
04. Hitunglah
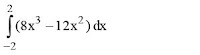
Jawab

Mengingat integral tentu dipeoleh dari konsep limit dan notasi sigma, maka sifat-sifat yang berlaku pada integral tentu sama dengan sifat-sifat yang berlaku pada limit dan notasi sigma tentu, yaitu:

Untuk lebih jelasnya akan diuraikan dalam contoh soal berikut ini :
05. Hitunglah
jawab

Thanks for reading & sharing .



